Comparacão dos modelos contínuo e discreto de Malthus e Verhulst
Palavras-chave:
Equações de diferenças, modelo de Malthus, modelo de Verhulst, bifurcaçãoResumo
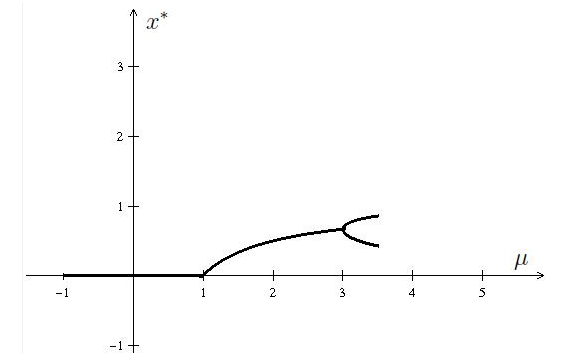
Neste trabalho consideramos dois importantes modelos de dinâmica populacional, modelo de Malthus e modelo de Verhuslt, em suas versões contínua e discreta. Iniciamos encontrando a solução geral e em seguida determinamos os pontos de equilíbrio desses modelos e sua estabilidade. Além disso, mostramos que não há diferença entre os pontos de equilíbrio do modelo de Malthus contínuo e discreto e no modelo de Verhulst discreto acontecem dois tipos de bifurcações que não ocorrem no contínuo.
Referências
BASSANEZZI, R. C. Ensino-aprendizagem com modelagem matemática: uma nova estratégia. São Paulo: Contexto, 2002.
BOYCE, W. E., DIPRIMA, R. C. Equações diferenciais elementares e problemas de valores de contorno. Rio de Janeiro: LTC, 2002.
LUÍS, R. D. G. Equações de diferenças e aplicações. Funchal, 2006.
Dissertação (Mestrado em Matemática) - Departamento de Matemática e Engenharias, Universidade da Madeira.
MONTEIRO, L. H. A. Sistemas dinâmicos. São Paulo: Livraria da Física, 2006.
RIZZO Jr., G. Segmentação e detecção de simetria em imagens via redes de mapas acoplados. São Paulo, 2006.
Dissertação (Mestrado em Engenharia) - Departamento de Engenharia de Telecomunicações e Controle, Universidade de São Paulo.
Downloads
Publicado
Como Citar
Edição
Seção
Licença
Proposta de Política para Periódicos de Acesso Livre
Autores que publicam nesta revista concordam com os seguintes termos:
- Autores mantém os direitos autorais e concedem à revista o direito de primeira publicação, com o trabalho simultaneamente licenciado sob a Licença Creative Commons Attribution que permite o compartilhamento do trabalho com reconhecimento da autoria e publicação inicial nesta revista.
- Autores têm autorização para assumir contratos adicionais separadamente, para distribuição não-exclusiva da versão do trabalho publicada nesta revista (ex.: publicar em repositório institucional ou como capítulo de livro), com reconhecimento de autoria e publicação inicial nesta revista.
- Autores têm permissão e são estimulados a publicar e distribuir seu trabalho online (ex.: em repositórios institucionais ou na sua página pessoal) a qualquer ponto antes ou durante o processo editorial, já que isso pode gerar alterações produtivas, bem como aumentar o impacto e a citação do trabalho publicado (Veja O Efeito do Acesso Livre).
