Data transformation under normality and heteroscedasticity

a simulation study

Abstract

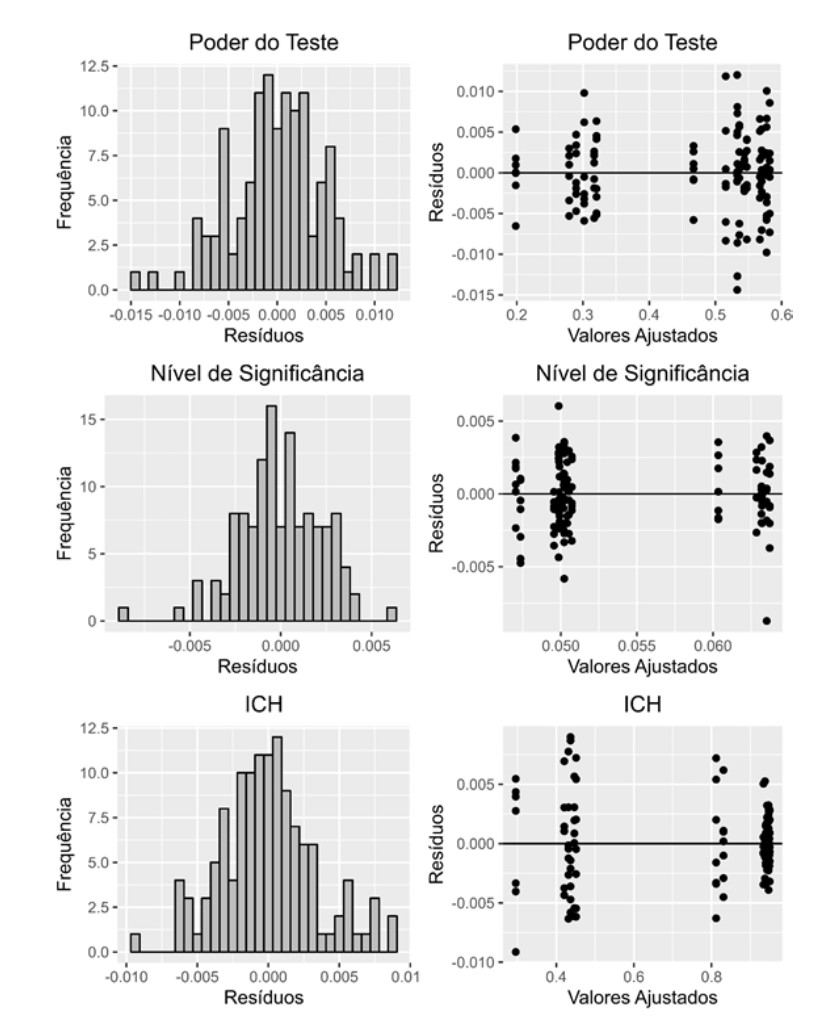
Analysis of Variance (ANOVA) is one of the most used inferential techniques in biological, ecological and agricultural sciences and it depends heavily on the assumption of equal variances along the treatments. Little is known about the properties of the F-test with different transformations under normality and heteroscedasticity. Therefore, this study aims to evaluate the impact of transformation on the power and significance level of F-test under heteroscedasticity. To do that, a simulation study was carried out using 6 transformations, 3 levels of non-constant variances, 7 repetitions and 10.000 simulated data sets. The mean proportions 5-5-5 and 5-5-6 were used to assess the significance level and power, respectively. Bartlett test was carried out on each simulated data set in order to define the Homogenization Capacity Index (HCI) to each transformation. The results were analyzed using ANOVA F-test at the level of 0.05 of the significance and compared using Tukey test after evaluating the presuppositions. Data transformation does not improve the power, significance level or the HCI at any level of heteroscedasticity. Since HCI stays around 40% after transformation, it's possible to have positive results in assumptions tests in spite of the quality of the test. The use of data transformation to handle heteroscedasticity in normal data is not an effective strategy and robust tests should be used.