Modelagem probabilística do índice IGPM12

Autores

  • Samantha Gouvêa Oliveira Doutoranda no programa de Estatística Aplicada e Biometria - Departamento de Estatística (DET/UFV) https://orcid.org/0009-0003-8789-1597
  • Luciano Gonçalves Batista Doutorando no programa de Estatística Aplicada e Biometria - Departamento de Estatística (DET/UFV)
  • Eduardo Campana Barbosa Docente do Departamento de Estatística (DET/UFV)
  • Paulo César Emiliano Docente do Departamento de Estatística (DET/UFV) https://orcid.org/0000-0002-1314-9002
  • Maurício Silva Lacerda Docente do Departamento de Apoio ao Ensino - Instituto Federal de Educação, Ciência e Tecnologia de Rondônia (DAPE/IFRO) https://orcid.org/0000-0003-1209-3956
  • Kamila Andrade de Oliveira Docente do Departamento de Engenharia Agrícola, Campus Chapadinha (DEA/UFMA) https://orcid.org/0000-0002-6401-4132

Palavras-chave:

Assimetria, curtose, máxima verossimiliança

Resumo

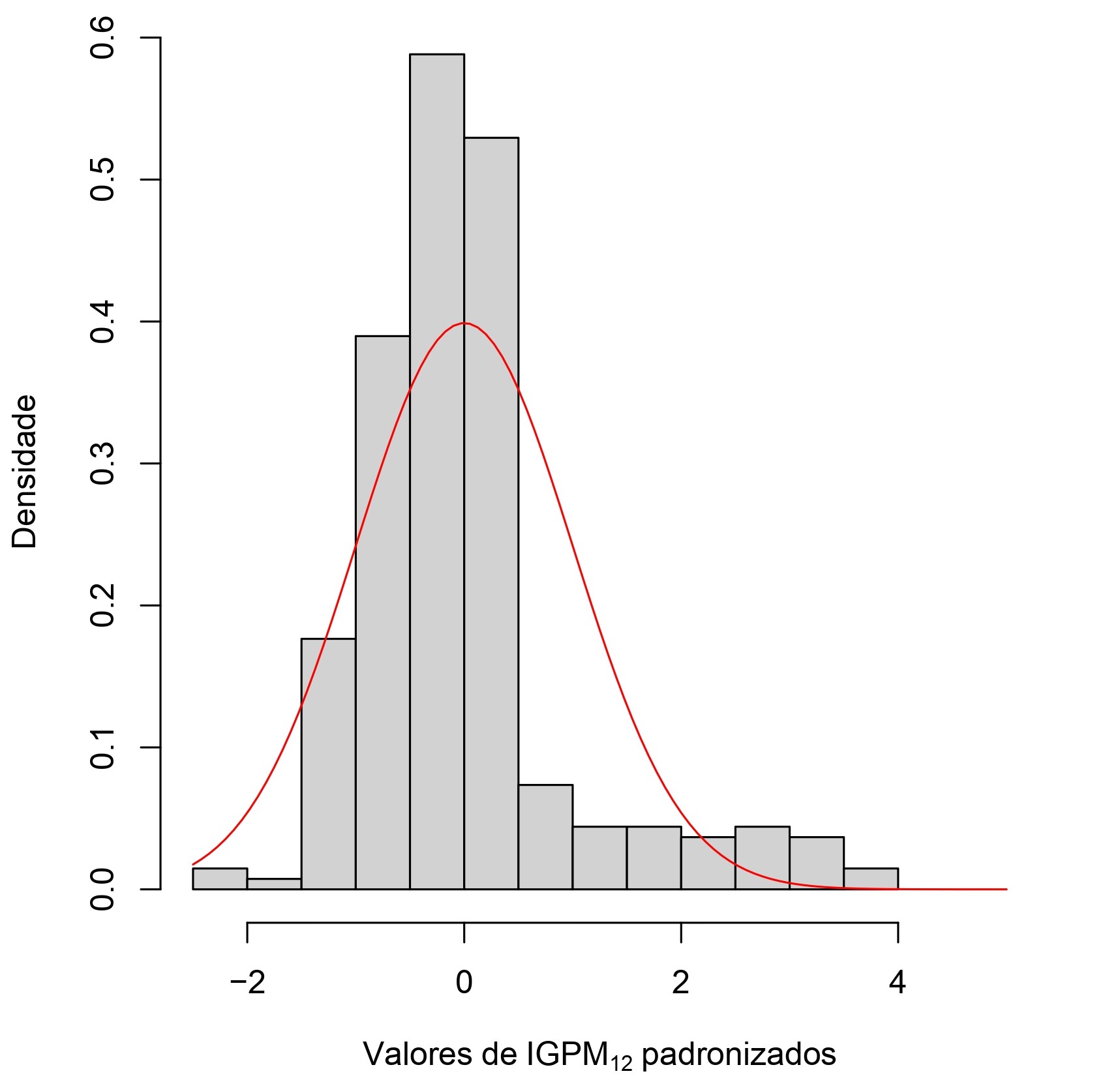
O objetivo desse trabalho foi ajustar uma distribuição aos dados de IGPM12 e estimar a probabilidade deste índice assumir determinados valores que podem ser prejudiciais para pessoas físicas, jurídicas e investidores que possuem compromissos ou ativos financeiros cuja remuneração é atrelada ao IGPM. Para escolher entre as distribuições normal, cauchy, logística e LS t-Student foram analisados o teste de Kolmogorov-Smirnov e o Critério de Informação de Akaike (AIC). O modelo LS t Student com parâmetros média 7,29, desvio-padrão 3,99 e nu 2,20 foi selecionado e com ele estimou-se as probabilidades de interesse. Concluiu-se que o cenário mais provável (p=62%) envolvia um reajuste desse índice entre 0% e 10% para os próximos 12 meses.

Referências

AKAIKE, H. A new look at the statistical model identification. IEEE Transactions on

Automatic Control, Notre Dame, v. 19, n. 6, p. 717-723, 1974.

CONOVER, W. J. Practical Nonparametric Statistical. John Wiley & Sons Inc., New York,

p.

De SOUZA, J. A. Para entender os índices de preços: uma visão moderna. ˆ Revista de

Economia Mackenzie, v. 2, n. 2, 2004.

EMILIANO, P. C.; VIVANCO, M. J. F.; MENEZES, F. S. Information criteria: How do they

behave in different models?. Computational Statistics & Data Analysis, v. 69, p. 141-153,

LENTH, R. V. Algorithm AS 243 — Cumulative distribution function of the non-central t

distribution. Applied Statistics, v. 38, n. 185–189, 1989.

MARSAGLIA G., TSANG W. W., WANG J. Evaluating Kolmogorov’s distribution. Journal

of Statistical Software, v. 8, n. 18, 2003.

MATTOS, A. A infla ̧c ̃ao brasileira. Uma abordagem pratica e moderna antes e depois do

choque. Petr ́opolis: Vozes, 1986.

MILLER, R. B. Maximum likelihood estimation and inference: with examples in R, SAS, and

ADMB. 1. ed. [S.l.]: Wiley, 2011.

MOOD, A. M.; GRAYBILL, F. A.; BOES, D. C. Introduction to the theory of statistics.

Singapore: McGraw-Hill, 1974. 564 p.

R CORE TEAM. R: a language and environment for statistical computing. R Foundation for

Statistical Computing, Vienna, Austria. 2023.

Downloads

Publicado

01-06-2024

Como Citar

Oliveira, S. G., Batista, L. G., Barbosa, E. C., Emiliano, P. C., Lacerda, M. S., & Oliveira, K. A. de. (2024). Modelagem probabilística do índice IGPM12. Sigmae, 13(2), 45–56. Recuperado de https://publicacoes.unifal-mg.edu.br/revistas/index.php/sigmae/article/view/2358

Edição

v. 13 n. 2 (2024): "Don't panic"

Seção

Estatística Aplicada

Licença

Proposta de Política para Periódicos de Acesso Livre


Autores que publicam nesta revista concordam com os seguintes termos:

    1. Autores mantém os direitos autorais e concedem à revista o direito de primeira publicação, com o trabalho simultaneamente licenciado sob a Licença Creative Commons Attribution que permite o compartilhamento do trabalho com reconhecimento da autoria e publicação inicial nesta revista.

    1. Autores têm autorização para assumir contratos adicionais separadamente, para distribuição não-exclusiva da versão do trabalho publicada nesta revista (ex.: publicar em repositório institucional ou como capítulo de livro), com reconhecimento de autoria e publicação inicial nesta revista.

  1. Autores têm permissão e são estimulados a publicar e distribuir seu trabalho online (ex.: em repositórios institucionais ou na sua página pessoal) a qualquer ponto antes ou durante o processo editorial, já que isso pode gerar alterações produtivas, bem como aumentar o impacto e a citação do trabalho publicado (Veja O Efeito do Acesso Livre).