Estimação sequencial bayesiana da proporção de loci em equilíbrio de Hardy-Weinberg

Resumo

A abordagem sequencial bayesiana utiliza-se amostras de tamanho variável, sem a necessidade de determinar o tamanho previamente. A decisão de interromper a amostragem é baseada em um critério de parada de comparação de riscos. Essa abordagem é útil em processos que envolvem amostras destrutivas, com alto tempo e custo financeiro, ou em situações em que o tamanho amostral não é definido por uma regra pré-estabelecida. Diante disso, essa
abordagem pode ser utilizada no contexto de genética de populações, para estimar a proporção de loci que estão em equilíbrio de Hardy-Weinberg (EHW), pois não há um padrão da quantidade de loci que são selecionados para a caracterização de uma população. Como existe um custo e tempo alto de operação laboratorial envolvidos, os loci são selecionados de acordo com os recursos disponíveis. O objetivo deste trabalho foi estimar a proporção de loci que estão em
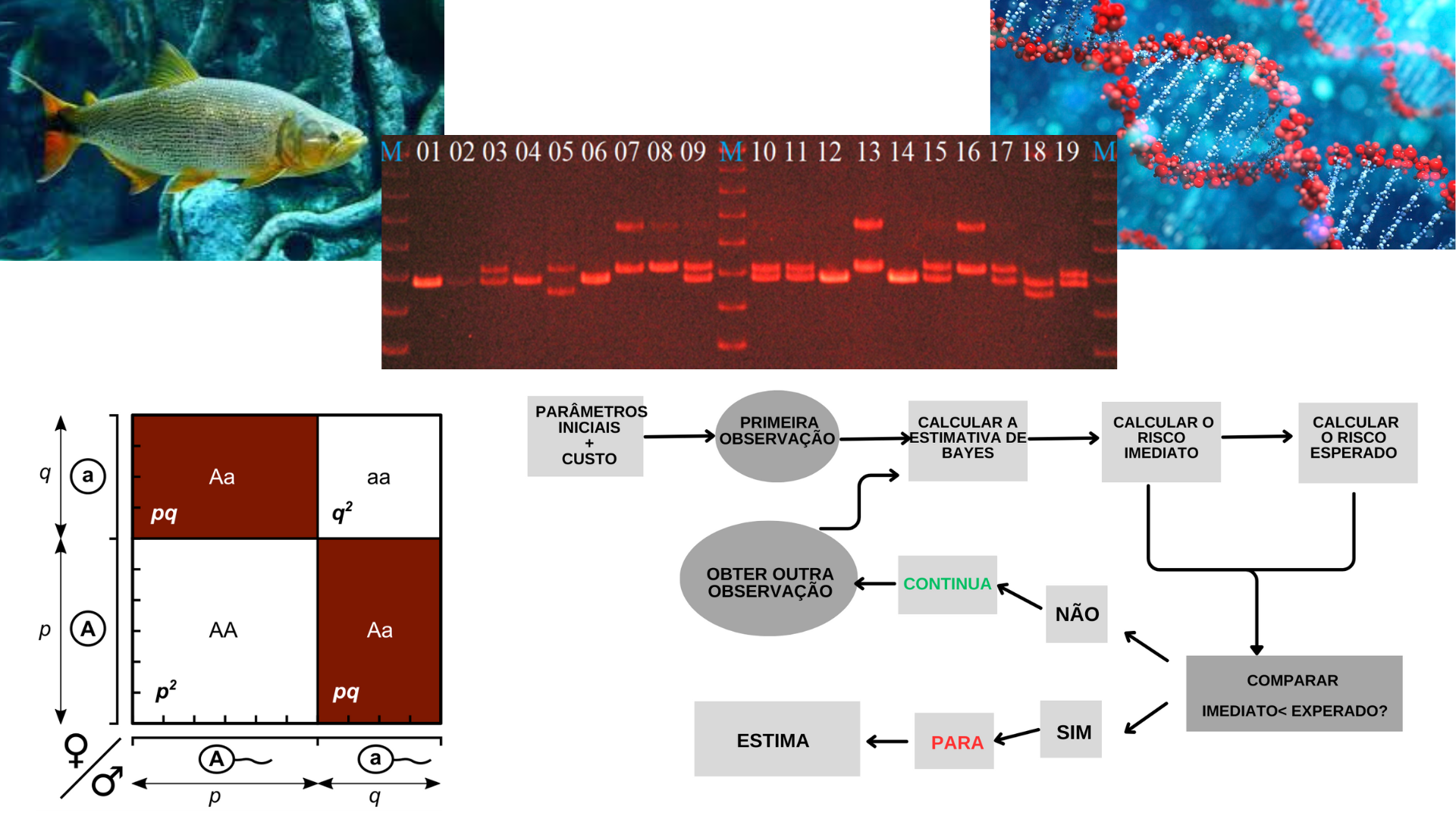
EHW, através da abordagem sequencial bayesiana, para caracterização da variabilidade genética do peixe dourado (Salminus brasiliensis). Cada locus foi verificado se estava em EHW, como a variável resposta é binária (está ou não em EHW) a distribuição de probabilidade associada é a binomial, então utilizou-se uma priori conjugada beta, cujos hiperparâmetros foram calculados com base em análises anteriores. Portanto, utilizando o critério de comparação dos riscos, após a avaliação do equilíbrio em 28 loci, o processo foi interrompido, e considerando uma função de perda quadrática, a estimação é dada pela média da distribuição beta a posteriori, o que resultou em uma estimativa de 50%.