O Primeiro ano da pandemia de SARS-CoV-2 em Maringá-PR

vigilância e avaliação em tempo real com um modelo de segunda derivada

Autores

  • Jefika Bezerra Universidade Federal do Amapá
  • Fernando Henrique Martins Fernandes Universidade Federal do Amapá https://orcid.org/0009-0001-0278-5951
  • Rodolfo de Souza Nascimento Universidade Estadual de Maringá https://orcid.org/0009-0005-5690-1769
  • Neylan Leal Dias Universidade Federal do Amapá
  • Jefferson Bezerra Universidade do Estado do Amapá

Palavras-chave:

Covid-19, Modelo exponencial, Regressão linear

Resumo

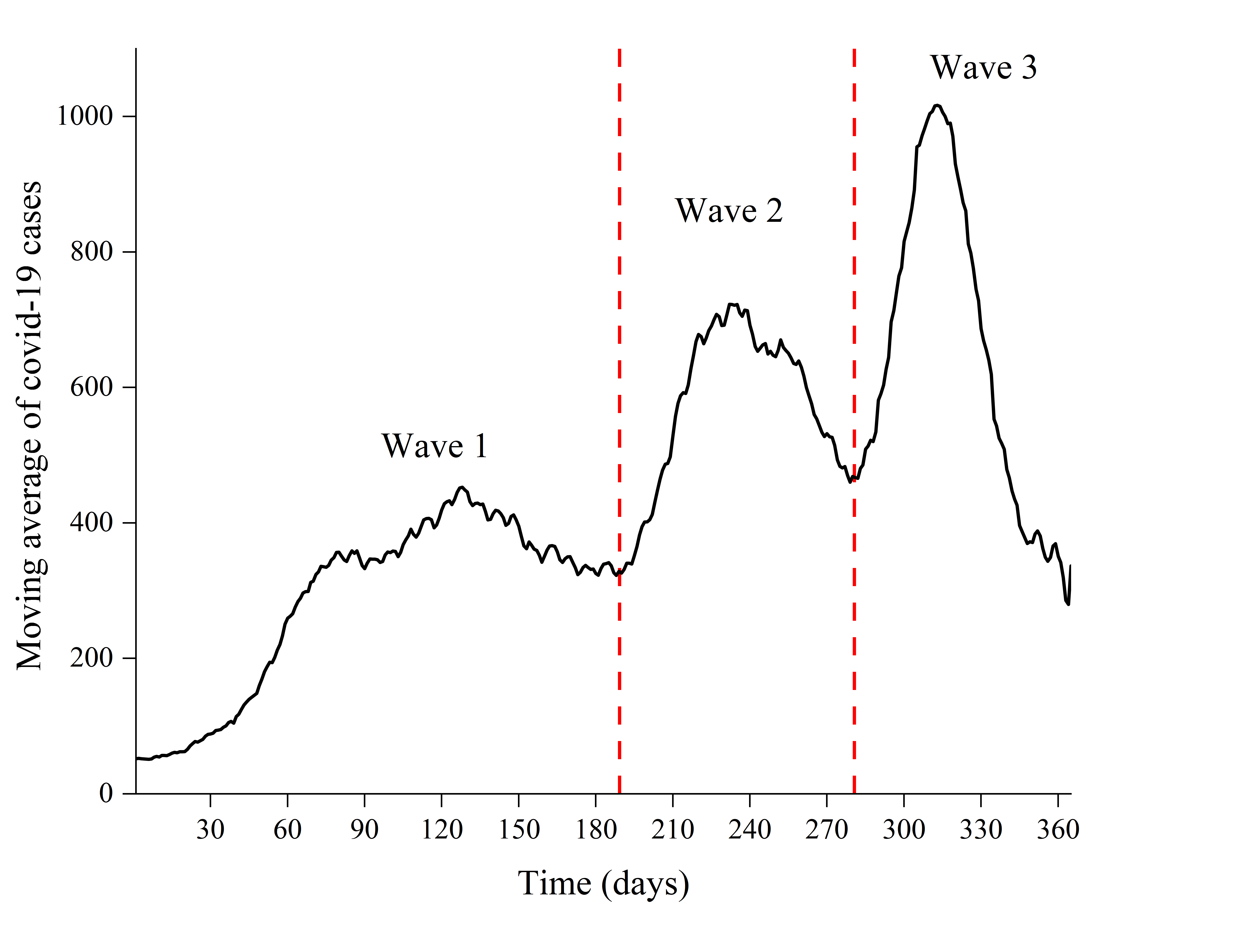
Este estudo investiga a dinâmica da pandemia de Covid-19 em Maringá, Brasil, durante seu primeiro ano e explora a utilidade de modelos matemáticos para a tomada de decisões. Originária de Wuhan, na China, a Covid-19 evoluiu rapidamente para uma pandemia global, chegando ao Brasil em fevereiro de 2020. Dados diários cumulativos de casos de abril de 2020 a abril de 2021 são analisados, revelando heterogeneidade temporal caracterizada por ondas distintas de casos de Covid-19. Modelos matemáticos, particularmente modelos exponenciais, são empregados para prever as tendências da pandemia, e sua precisão é avaliada. Os resultados sublinham a eficácia de intervenções como o recolher obrigatório e a imposição de máscaras para moldar a dinâmica da transmissão. A análise da velocidade e da aceleração da infeção demonstra o impacto dos feriados e das intervenções na propagação do vírus. É introduzido um parâmetro, Pi, para avaliar a adequação do modelo, indicando uma boa concordância com os dados do mundo real durante a maior parte do período de estudo. Esta investigação sublinha o papel crucial da modelação matemática na gestão da pandemia e fornece informações valiosas aos decisores e às partes interessadas para atenuar o impacto de surtos como o da Covid-19. Compreender a dinâmica temporal das pandemias é essencial para implementar intervenções eficazes e salvaguardar a saúde pública. Globalmente, este estudo contribui para o nosso conhecimento das estratégias de controle da pandemia e da sua aplicação em futuros surtos

Biografia do Autor

Jefika Bezerra , Universidade Federal do Amapá

Está cursando licenciatura em Matemática pela Universidade Federal do Amapá, vinculado ao Departamento de Ciências Exatas e Tecnológicas (DCET), concluiu o Ensino Médio na Escola Estadual Frei Constâncio. Possui vivência como instrutora particular de matemática, trabalhando com alunos do ensino básico e oferecendo serviços de suporte à distância.

Fernando Henrique Martins Fernandes , Universidade Federal do Amapá

Possui graduação em Engenharia de Energias Renováveis pela Universidade Federal da Paraíba(2017), graduação em Engenharia Elétrica pela Universidade Federal da Paraíba(2018) e ensino-medio-segundo-graupelo Colégio Vega(2007).

Neylan Leal Dias , Universidade Federal do Amapá

Curso de Licenciatura Plena em Matemática (2013) - UNIFAP, Mestrado em Matemática Aplicada e Computacional (2017) - FCT/Unesp e Atualmente Cursando Doutorado em Engenharia Mecânica na FEB/Unesp com pesquisa em Modelagem e Controle de Sistemas Biológicos. Foi Professor Formador da EAD/UNIFAP-Oiapoque em várias disciplinas e Professor Substituto do Colegiado de Matemática/Unifap entre 09/2019 a 09/2021. Professor (Aluno de Doutorado) na Unesp/FEB das disciplinas Estatística (2020.2) e Calculo Diferencial e Integral (2021.1). Foi professor Substituto na UEMA (Univ. Estadual do Maranhão) onde já ministrou disciplinas de Estatística, Física Aplicada, Matemática Aplicada, Fundamentos de MecÂnica (Fisica I ? Prática e Experimental), Eletrotécnica (Eletricidade e Magnetismo) e Teoria dos Números. Atualmente é Professor Efetivo Dedicação Exclusiva da Universidade Federal do Amapá - UNIFAP no Campus Binacional junto ao Colegiado de Biologia nas disciplinas de Matemática, Física e Bioestatística. Tem experiência na área de Matemática, com ênfase em Modelagem Matemática de Sistemas Biológicos e Métodos Numéricos, atuando principalmente nos seguintes temas: Modelagem Matemática, Equações Diferenciais, Dinâmica de Populações, Diferenças Finitas, Modelagem do Sars-Cov-2. Atualmente Concluindo a tese de Doutorado em Dinâmica e Controle de sistemas Não-Lineares na Modelagem matemática da Bioacumulação de mercúrio a partir do modelo de predação tipo Lotka e Volterra generalizado (Multi-Espécies) levando-se em conta Sensibilidade dos parâmetros e a Contribuição de termos de Ordem Fracionária.

Referências

CHANG, J. T.; KAPLAN, E. H. Modeling local coronavirus outbreaks. European journal of operational research, 304, n. 1, p. 57-68, 2023.

CHEN, X.; YU, B. First two months of the 2019 Coronavirus Disease (COVID-19) epidemic in China: real-time surveillance and evaluation with a second derivative model. Global health research and policy, 5, n. 1, p. 1-9, 2020.

DA SILVA, C. M.; DA SILVA, P. J.; DE ALBUQUERQUE, I. C. A.; DO NASCIMENTO JUNIOR, A. J. et al. Ajuste de funções matemáticas de crescimento aos números de casos de pessoas contaminadas com o COVID-19 no Brasil: uma abordagem para o ensino médio. Research, Society and Development, 10, n. 16, p. e351101623881-e351101623881, 2021.

DOS REIS, M. M.; SEGALA, V. C. S.; BELOTO, A. B. Prevalência de sequelas respiratórias e não respiratórias pós-covid-19 em habitantes da cidade de Maringá-PR. Anais do XII Encontro de Produção Científica da UNICESUMAR - Universidade Cesumar, p.1-3, 2021. ISSN: 2594-4991. ISBN: 978-65-5615-456-5. Disponível em: https://www.unicesumar.edu.br/anais-epcc-2021/wp-content/uploads/sites/236/2021/11/692.pdf.

G1. Carnaval 2020: veja datas. 2020a. Disponível em: https://g1.globo.com/carnaval/2020/noticia/2019/03/18/carnaval-2020-veja-datas.ghtml. Acesso em: 25/09/23.

G1. Coronavírus: Prefeitura de Maringá decreta situação de emergência e determina fechamento de comércio. 2020b. Disponível em: https://g1.globo.com/pr/norte-noroeste/noticia/2020/03/18/coronavirus-prefeitura-decreta-situacao-de-emergencia-e-determina-fechamento-de-comercio.ghtml.

MOURA, G. G.; NASCIMENTO, C. R. R.; FERREIRA, J. M. COVID-19: Reflections on the crisis, transformation, and interactive processes under development. Trends in Psychology, 29, n. 2, p. 375-394, 2021.

PAVLYUTIN, M.; SAMOYAVCHEVA, M.; KOCHKAROV, R.; PLESHAKOVA, E. et al. COVID-19 spread forecasting, mathematical methods vs. machine learning, Moscow case. Mathematics, 10, n. 2, p. 195, 2022.

PEDROSO, M. C.; PIRES, J. T.; MALIK, A. M.; PEREIRA, A. J. R. HCFMUSP: Resilience in response to the COVID-19 pandemic. Revista de Administração Contemporânea, 25, p. e200245, 2021.

PREFEITURA DE MARINGÁ. Linha do tempo: 2020. 2020a. Disponível em: http://www.maringa.pr.gov.br/sistema/arquivos/a8be15d2f353.pdf. Acesso em: 25/09/2023.

PREFEITURA DE MARINGÁ. NOTA OFICIAL: Confirmado primeiro caso de coronavírus em Maringá. 2020b. Disponível em: https://shorturl.at/esKT7. Acesso em: 25/09/2023.

QUEIROZ, H. R.; PEREIRA, D. D.; DE OLIVEIRA, R. R.; MATTA, A. C. G. et al. PERFIL EPIDEMIOLÓGICO DOS CASOS CONFIRMADOS DE COVID-19 NOTIFICADOS NA CIDADE DE MARINGÁ. Revista Multidisciplinar em Saúde, 2, n. 4, p. 15-15, 2021.

RIBEIRO, H. V.; SUNAHARA, A. S.; SUTTON, J.; PERC, M. et al. City size and the spreading of COVID-19 in Brazil. PloS one, 15, n. 9, p. e0239699, 2020.

SAÚDE. Boletim epidemiológico covid-19 diário. 2020. Disponível em: http://www.maringa.pr.gov.br/saude/?cod=boletimcorona/2.

SUNAHARA, A. S.; PESSA, A. A.; PERC, M.; RIBEIRO, H. V. Complexity of the COVID-19 pandemic in Maringá. Scientific Reports, 13, n. 1, p. 12695, 2023.

UNIVERSIDADE ABERTA DO SUS. Coronavírus: Brasil confirma primeiro caso da doença. 2020. Disponível em: https://shorturl.at/lnyC7. Acesso em: 25/09/23.

Downloads

Publicado

31-12-2023

Como Citar

Bezerra , J. ., Fernandes , F. H. M. ., Nascimento , R. de S. ., Dias , N. L. ., & Bezerra , J. (2023). O Primeiro ano da pandemia de SARS-CoV-2 em Maringá-PR: vigilância e avaliação em tempo real com um modelo de segunda derivada. Sigmae, 12(3), 51–59. Recuperado de https://publicacoes.unifal-mg.edu.br/revistas/index.php/sigmae/article/view/2257

Edição

v. 12 n. 3 (2023): Número especial: 67ª RBRAS e 20° SEAGRO

Seção

Estatística Aplicada

Licença

Proposta de Política para Periódicos de Acesso Livre


Autores que publicam nesta revista concordam com os seguintes termos:

    1. Autores mantém os direitos autorais e concedem à revista o direito de primeira publicação, com o trabalho simultaneamente licenciado sob a Licença Creative Commons Attribution que permite o compartilhamento do trabalho com reconhecimento da autoria e publicação inicial nesta revista.

    1. Autores têm autorização para assumir contratos adicionais separadamente, para distribuição não-exclusiva da versão do trabalho publicada nesta revista (ex.: publicar em repositório institucional ou como capítulo de livro), com reconhecimento de autoria e publicação inicial nesta revista.

  1. Autores têm permissão e são estimulados a publicar e distribuir seu trabalho online (ex.: em repositórios institucionais ou na sua página pessoal) a qualquer ponto antes ou durante o processo editorial, já que isso pode gerar alterações produtivas, bem como aumentar o impacto e a citação do trabalho publicado (Veja O Efeito do Acesso Livre).