Modelos Aditivos Parcialmente Lineares
Palabras clave:
Modelos Aditivos Parcialmente Lineares, B-Splines, Máxima Verossimilhança PenalizadaResumen
No presente trabalho são apresentados os modelos aditivos parcialmente lineares, isto é, uma extensão dos modelos lineares que incorporam componentes não lineares para modelar
relacionamentos mais complexos entre variáveis independentes e a variável resposta. O objetivo do trabalho é estudar tais modelos e implementar um algoritmo que possibilite a estimação
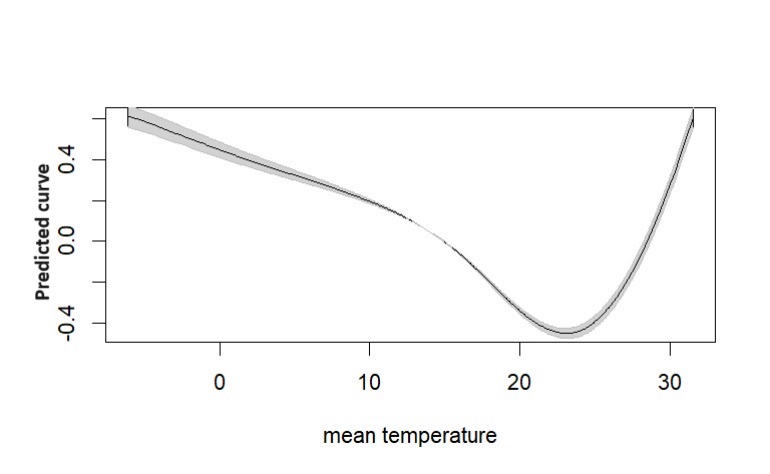
dos parâmetros. São utilizados os B-Splines para descrever as componentes não paramétricas. Considerando a função de verossimilhança penalizada, obtemos os estimadores de máxima verossimilhança bem como a matriz de informação de Fisher, sendo esta utilizada para obtenção das estimativas dos desvios-padrão dos estimadores dos parâmetros. Além disso, é utilizado o critério de informação Bayesiano para seleção dos parâmetros de suavização. Foram realizados estudos de simulação para verificar as propriedades assintóticas dos estimadores de máxima verossimilhança. Por fim, para ilustrar a utilizade do modelo proposto, ajustamos o mesmo a um conjunto de dados sobre mortalidade na cidade de Milão (Itália) utilizando como variáveis explicativas não lineares temperatura e humidade e como lineares o número de partículas em suspensão no ar e o tempo (em número de dias).
Citas
DAVISON, A. C.; HINKLEY, D. V. Bootstrap methods and their application. New York:
Cambridge University Press, 1997.
DE BOOR, C. A practical guide to splines, revised. Berlin: Springer, 2001.
EILERS, P. H. C.; MARX, B. D. Flexible smoothing with B-splines and penalties. Statistical
Science, 11(2), 89-121, 1996.
FARAWAY, J. J. Extending the Linear Model with R: Generalized Linear, Mixed Effects and
Nonparametric Regression Models, sec. ed., Boca Raton: CRC Press, 2016.
GREEN, P. J.; SILVERMAN, B. W. Nonparametric Regression and Generalized Linear
Models: A roughness penalty approach. London: Chapman and Hall, 1994.
HASTIE, T.; TIBSHIRANI, R. Generalized Additive Models. London: Chapman and Hall,
IBACACHE-PULGAR, G.; PAULA, G. A.; CYSNEIROS, F. J. A. Semiparametric additive
models under symmetric distributions. Test, 22, 103-121, 2013.
LIU, X.; WANG, L.; LIANG, H. Estimation and Variable Selection for Semiparametric
Additive Partial Linear Models. Stat Sin., 21 (3),1225-1248, 2011.
R CORE TEAM. R: A language and environment for statistical computing. R Foundation for
Statistical Computing, Vienna, Austria, 2023. Dispon ́ıvel em: http://www.R-project.org.
RACINE, J. S.; SU, L.; ULLAH, A. The Oxford Handbook of Applied Nonparametric and
Semiparametric Econometrics and Statistics. New York: Oxford University Press, 2014.
RUPPERT, D.; WAND, M. P.; CARROL, R. J. Semiparametric Regression. New York:
Cambridge Univ. Press, 2003.
WANG, B.; FANG, Y.; LIAN, H.; LIANG, H. Additive partially linear models for massive
heterogeneous data. Electronic Journal of Statistics, 13, 391-431, 2019.
WOOD, S. N. Generalized Additive Models: an introduction with R. Second Edition. Boca
Raton: Chapman and Hall, 2017.
Descargas
Publicado
Cómo citar
Número
Sección
Licencia
Proposta de Política para Periódicos de Acesso Livre
Autores que publicam nesta revista concordam com os seguintes termos:
- Autores mantém os direitos autorais e concedem à revista o direito de primeira publicação, com o trabalho simultaneamente licenciado sob a Licença Creative Commons Attribution que permite o compartilhamento do trabalho com reconhecimento da autoria e publicação inicial nesta revista.
- Autores têm autorização para assumir contratos adicionais separadamente, para distribuição não-exclusiva da versão do trabalho publicada nesta revista (ex.: publicar em repositório institucional ou como capítulo de livro), com reconhecimento de autoria e publicação inicial nesta revista.
- Autores têm permissão e são estimulados a publicar e distribuir seu trabalho online (ex.: em repositórios institucionais ou na sua página pessoal) a qualquer ponto antes ou durante o processo editorial, já que isso pode gerar alterações produtivas, bem como aumentar o impacto e a citação do trabalho publicado (Veja O Efeito do Acesso Livre).
