Partially Linear Additive Models
Keywords:
Partially Linear Additive Models, B-Splines, Penalized Maximum LikelihoodAbstract
In the present work, partially linear additive models are presented. This means an extension of linear models that incorporate non-linear components to model more complex relationships between independent variables and the response variable. The goal of the work is to study these models and implement an algorithm that enables parameter estimation. B-Splines are used
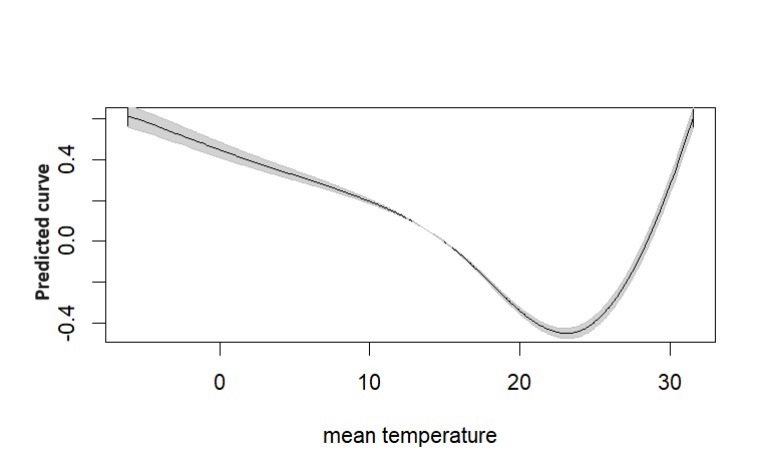
to describe the non-parametric components. Considering the penalized likelihood function, we obtain maximum likelihood estimators as well as the Fisher information matrix, which is used to obtain standard error estimates for the parameter estimators. Additionally, the Bayesian information criterion is used for parameter smoothing selection. Simulation studies were conducted to verify the asymptotic properties of the maximum likelihood estimators. Finally, to illustrate the utility of the proposed model, it was applied to a dataset on mortality in the city of Milan, Italy. Non-linear explanatory variables include temperature and humidity, while linear variables include the number of suspended particles in the air and time (in days).
References
DAVISON, A. C.; HINKLEY, D. V. Bootstrap methods and their application. New York:
Cambridge University Press, 1997.
DE BOOR, C. A practical guide to splines, revised. Berlin: Springer, 2001.
EILERS, P. H. C.; MARX, B. D. Flexible smoothing with B-splines and penalties. Statistical
Science, 11(2), 89-121, 1996.
FARAWAY, J. J. Extending the Linear Model with R: Generalized Linear, Mixed Effects and
Nonparametric Regression Models, sec. ed., Boca Raton: CRC Press, 2016.
GREEN, P. J.; SILVERMAN, B. W. Nonparametric Regression and Generalized Linear
Models: A roughness penalty approach. London: Chapman and Hall, 1994.
HASTIE, T.; TIBSHIRANI, R. Generalized Additive Models. London: Chapman and Hall,
IBACACHE-PULGAR, G.; PAULA, G. A.; CYSNEIROS, F. J. A. Semiparametric additive
models under symmetric distributions. Test, 22, 103-121, 2013.
LIU, X.; WANG, L.; LIANG, H. Estimation and Variable Selection for Semiparametric
Additive Partial Linear Models. Stat Sin., 21 (3),1225-1248, 2011.
R CORE TEAM. R: A language and environment for statistical computing. R Foundation for
Statistical Computing, Vienna, Austria, 2023. Dispon ́ıvel em: http://www.R-project.org.
RACINE, J. S.; SU, L.; ULLAH, A. The Oxford Handbook of Applied Nonparametric and
Semiparametric Econometrics and Statistics. New York: Oxford University Press, 2014.
RUPPERT, D.; WAND, M. P.; CARROL, R. J. Semiparametric Regression. New York:
Cambridge Univ. Press, 2003.
WANG, B.; FANG, Y.; LIAN, H.; LIANG, H. Additive partially linear models for massive
heterogeneous data. Electronic Journal of Statistics, 13, 391-431, 2019.
WOOD, S. N. Generalized Additive Models: an introduction with R. Second Edition. Boca
Raton: Chapman and Hall, 2017.
Downloads
Published
How to Cite
Issue
Section
License
Proposta de Política para Periódicos de Acesso Livre
Autores que publicam nesta revista concordam com os seguintes termos:
- Autores mantém os direitos autorais e concedem à revista o direito de primeira publicação, com o trabalho simultaneamente licenciado sob a Licença Creative Commons Attribution que permite o compartilhamento do trabalho com reconhecimento da autoria e publicação inicial nesta revista.
- Autores têm autorização para assumir contratos adicionais separadamente, para distribuição não-exclusiva da versão do trabalho publicada nesta revista (ex.: publicar em repositório institucional ou como capítulo de livro), com reconhecimento de autoria e publicação inicial nesta revista.
- Autores têm permissão e são estimulados a publicar e distribuir seu trabalho online (ex.: em repositórios institucionais ou na sua página pessoal) a qualquer ponto antes ou durante o processo editorial, já que isso pode gerar alterações produtivas, bem como aumentar o impacto e a citação do trabalho publicado (Veja O Efeito do Acesso Livre).



