Bayesian sequential estimation of the proportion of loci in Hardy-Weinberg equilibrium

Abstract

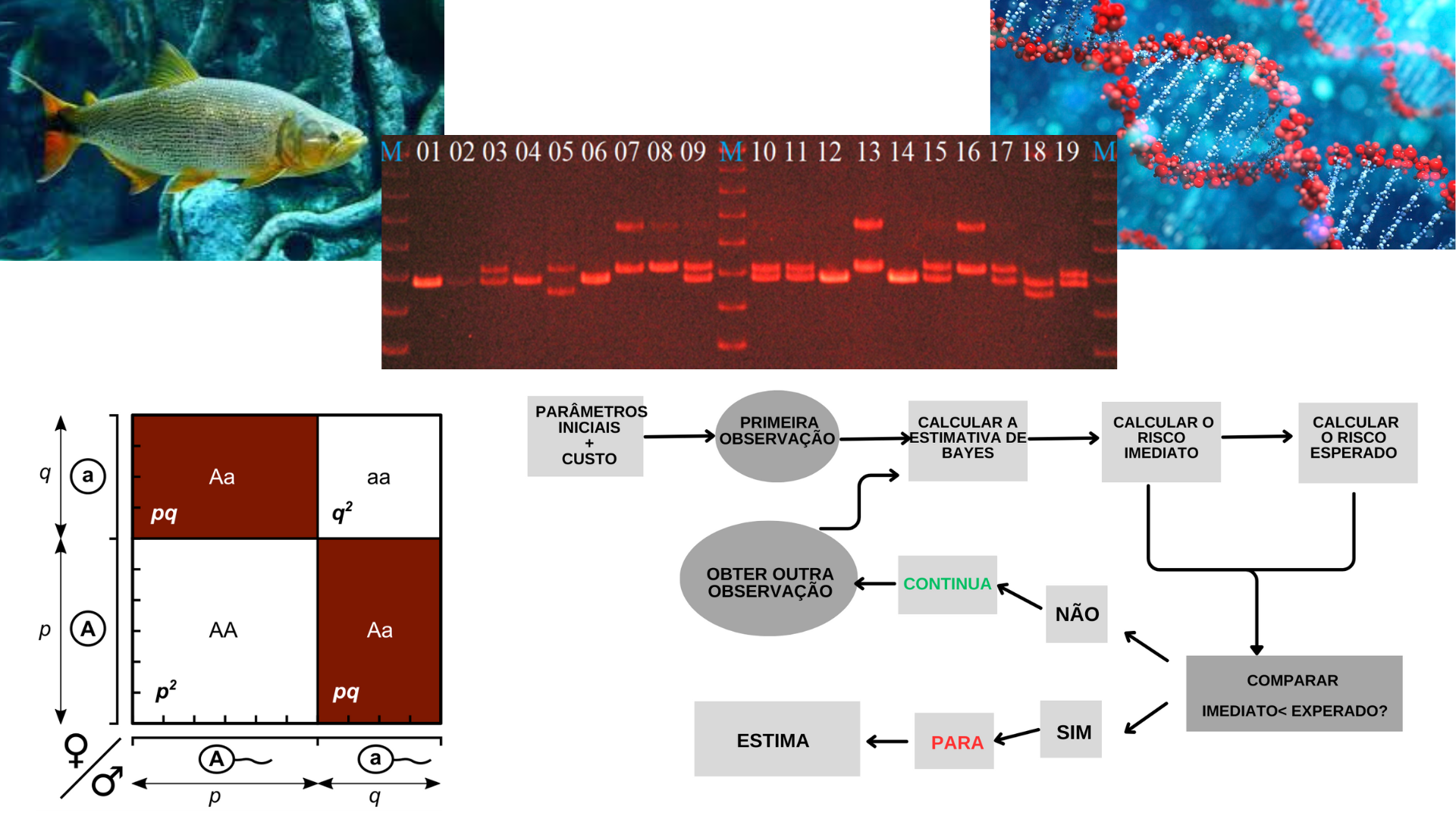
The Bayesian sequential approach uses samples of variable size, without the need to determine the size beforehand. The decision to stop sampling is based on a stopping criterion that compares risks. This approach is useful in processes involving destructive samples, with high time and financial costs, or in situations where the sample size is not defined by a pre-established rule. Given this, this approach can be used in the context of population genetics to estimate the proportion of loci in Hardy-Weinberg equilibrium (HWE), as there is no standard for the quantity of loci selected for population characterization. Due to the high cost and time involved in laboratory operations, loci are selected based on available resources. The objective of this study was to estimate the proportion of loci in HWE using the Bayesian sequential approach to characterize the genetic variability of the golden dorado (Salminus brasiliensis). Each locus was checked for HWE. Since the response variable is binary (in HWE or not), the associated probability distribution is binomial. A conjugate beta prior was used, whose hyperparameters were calculated based on previous analyses. Therefore, using the risk comparison criterion, after evaluating equilibrium in 28 loci, the process was terminated. Considering a quadratic loss function, the estimation is given by the mean of the posterior beta distribution, resulting in an estimate of 50%.