Probabilistic modeling of the IPCA12 index

Authors

  • Luciano Gonçalves Batista Doutorando no programa de Estatística Aplicada e Biometria - Departamento de Estatística (DET/UFV) https://orcid.org/0000-0001-5785-1568
  • Samantha Gouvêa Oliveira Doutoranda no programa de Estatística Aplicada e Biometria - Departamento de Estatística (DET/UFV)
  • Eduardo Campana Barbosa Docente do Departamento de Estatística (DET/UFV)
  • Paulo César Emiliano Docente do Departamento de Estatística (DET/UFV) https://orcid.org/0000-0002-1314-9002
  • Maurício Silva Lacerda Docente do Departamento de Apoio ao Ensino - Instituto Federal de Educação, Ciência e Tecnologia de Rondônia (DAPE/IFRO) https://orcid.org/0000-0003-1209-3956
  • Kamila Andrade de Oliveira Docente do Departamento de Engenharia Agrícola, Campus Chapadinha (DEA/UFMA). https://orcid.org/0000-0002-6401-4132

Keywords:

Asymmetry, kurtosis, maximum likelihood

Abstract

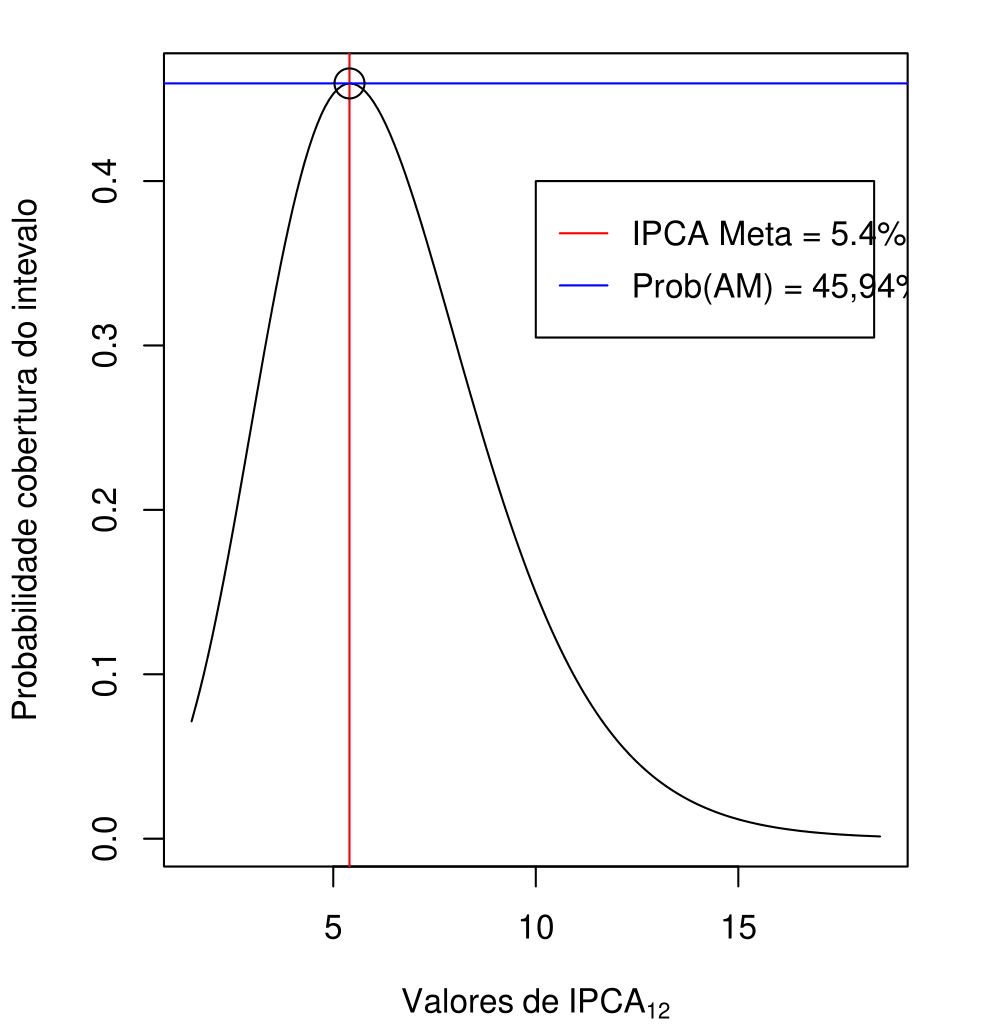
The objective of this work was to fit a distribution to the IPCA12 dataset and estimate the probability of this index remaining within the confidence limits established by the Central Bank of Brazil for year 2024, which are 3% +- 1.5%. To choose between the log-normal, Gamma, and Weibull distributions, Kolmogorov-Smirnov test, and the Akaike Information Criterion (AIC) were analyzed. The Gamma model with parameters alfa 5.81 and beta 1.09 was selected, and it was estimated that the probability of the true value of IPCA staying within the confidence interval established by the Central Bank for the year 2024 would be 25.45%. Furthermore, maintaining a margin of +- 1.5%, it was possible to conclude that the IPCA value or target that would maximize coverage of the range should be 5.4% instead of 3%. More specifically: P(5.4% - 1.5% <= IPCA12 <= 5.4% + 1.5%) = 45.94%.

References

AKAIKE, H. A new look at the statistical model identification. IEEE Transactions on

Automatic Control, Notre Dame, v. 19, n. 6, p. 717-723, 1974.

BARROS, R. P. de; NERI, M. M., R. Pobreza e inflação no Brasil: Uma análise agregada.

Economia Brasileira em Perspectiva. Rio de Janeiro: IPEA, vol 1, 1996. 838 p.

CONOVER, W. J. Practical Nonparametric Statistical. John Wiley & Sons Inc., New York,

p.

DELFIM NETTO, A. Sobre as metas inflacionárias. Revista de Economia Aplicada, v. 3, n. 3,

EMILIANO, P. C.; VIVANCO, M. J. F.; MENEZES, F. S. Information criteria: How do they

behave in different models?. Computational Statistics & Data Analysis, v. 69, p. 141-153, 2014.

FERREIRA, T. P.; FIGUEIREDO F. M. R. Os preços administrados e a inflação no Brasil.

Banco Central do Brasil Trabalhos para Discussão, n. 59, Brasília, dez. 2002.

FERREIRA, T.P.; PETRASSI,M. B. S. Regime de metas de inflação: resenha sobre a

experiência internacional. Banco Central do Brasil. Notas Técnicas, no 30, Brasília, nov., 2002.

MARSAGLIA G., TSANG W. W., WANG J. Evaluating Kolmogorov’s distribution. Journal of

Statistical Software, v. 8, n. 18, 2003.

MILLER, R. B. Maximum likelihood estimation and inference: with examples in R, SAS, and

ADMB. 1. ed. [S.l.]: Wiley, 2011.

MOOD, A. M.; GRAYBILL, F. A.; BOES, D. C. Introduction to the theory of statistics.

Singapore: McGraw-Hill, 1974. 564 p.

R CORE TEAM. R: a language and environment for statistical computing. R Foundation for

Statistical Computing, Vienna, Austria. 2023.

Downloads

Published

21-08-2024

How to Cite

Batista, L. G., Oliveira, S. G., Barbosa, E. C., Emiliano, P. C., Lacerda, M. S., & Oliveira, K. A. de. (2024). Probabilistic modeling of the IPCA12 index. Sigmae, 13(2), 33–44. Retrieved from https://publicacoes.unifal-mg.edu.br/revistas/index.php/sigmae/article/view/2359

Issue

Vol. 13 No. 2 (2024): "Don't panic"

Section

Applied Statistics

License

Proposta de Política para Periódicos de Acesso Livre


Autores que publicam nesta revista concordam com os seguintes termos:

    1. Autores mantém os direitos autorais e concedem à revista o direito de primeira publicação, com o trabalho simultaneamente licenciado sob a Licença Creative Commons Attribution que permite o compartilhamento do trabalho com reconhecimento da autoria e publicação inicial nesta revista.

    1. Autores têm autorização para assumir contratos adicionais separadamente, para distribuição não-exclusiva da versão do trabalho publicada nesta revista (ex.: publicar em repositório institucional ou como capítulo de livro), com reconhecimento de autoria e publicação inicial nesta revista.

  1. Autores têm permissão e são estimulados a publicar e distribuir seu trabalho online (ex.: em repositórios institucionais ou na sua página pessoal) a qualquer ponto antes ou durante o processo editorial, já que isso pode gerar alterações produtivas, bem como aumentar o impacto e a citação do trabalho publicado (Veja O Efeito do Acesso Livre).